Contents
泊松重建 (Possion Reconstruction)
Reconstructing 3D surfaces from point samples
三维指示函数拟合
输入:有法向量的点集\(S\)(有向点云)
样本点 \(s\in{S}\) 位于未知模型 \(M\) 的表面 \(∂M\) 附in近,且必须包含两个属性: \(s.p\)(坐标)和 \(s.\overrightarrow{N}\)(朝内的法向)。
输出:指示函数(indicator function)\(\chi\),用于确定表里
隐函数拟合

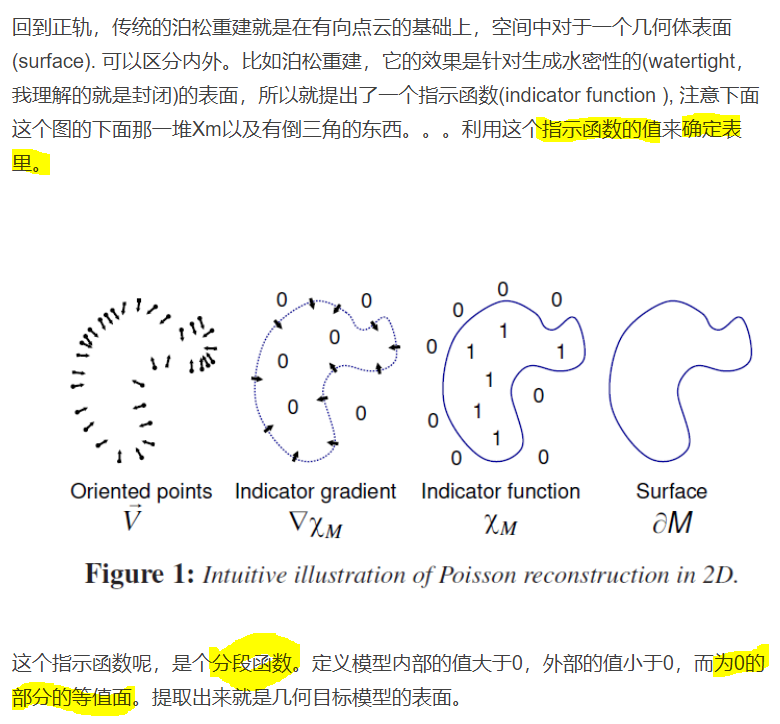
Key insight: The gradient of the indicator function is a vector field that is zero almost everywhere (since the indicator function is constant almost everywhere), except at points near the surface, where it is equal to the inward surface normal.
Thus, the oriented point samples can be viewed as samples of the gradient of the model’s indicator function.
求解方法
-
证明:平滑指示函数的梯度 等于 平滑表面法向场得到的向量场
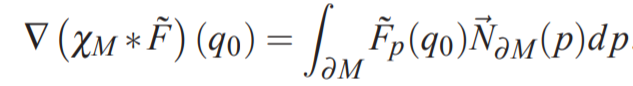
其中\(\overrightarrow N_{\partial_{M}}(p)\)为\(p\in∂M\)处的法向量。即\(\nabla\widetilde\chi=\overrightarrow{V}\)
-
用离散求和近似的方式去计算曲面积分,算出向量场\(\overrightarrow{V}\):
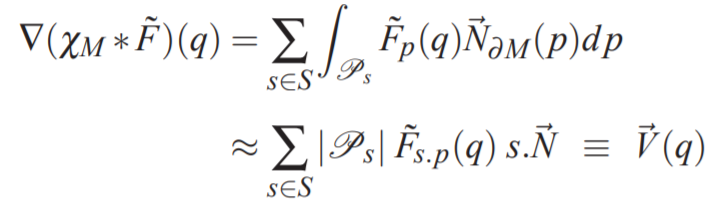
其中用于平滑的滤波器\(\overrightarrow{F}\)要满足两个条件:1.足够窄(避免数据过拟合)2. 足够宽(\(\mathcal P_S\)处的积分能较好地被the value at s.p scaled by the patch area估计)。可选:方差约等于采样分辨率的高斯滤波器。
-
向量场是不可积的,只能近似。因此利用最小二乘估计,引入散度算子组成泊松方程。求\(\chi\)即解泊松方程:
\[\Delta\widetilde\chi\equiv\nabla^2\widetilde\chi\equiv\nabla\cdot{\nabla\widetilde\chi}=\nabla\cdot{\overrightarrow{V}}\]即\(\chi\)的拉普拉斯算子(梯度的散度)等于向量场的散度。
等值面提取
2.1 计算等值面值(isovalue)
evaluating \(\widetilde\chi\) at the sample positions and use the average of the values for isosurface extraction:
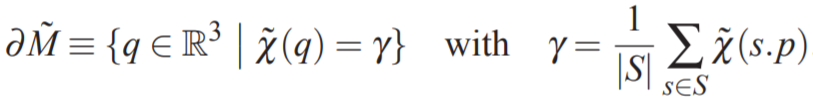
2.2 通过定义在八叉树上的Marching Cubes方法提取等值面
【附:相关数学知识】
泊松方程定义与求解(图像场景)




矢量分析:梯度、散度、旋度
向量场A,数量场u:
▽称为汉密尔顿算子; ▽·▽=△,△称为拉普拉斯算子。
【梯度】▽u 【散度】▽·A(点乘结果为数)


本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)


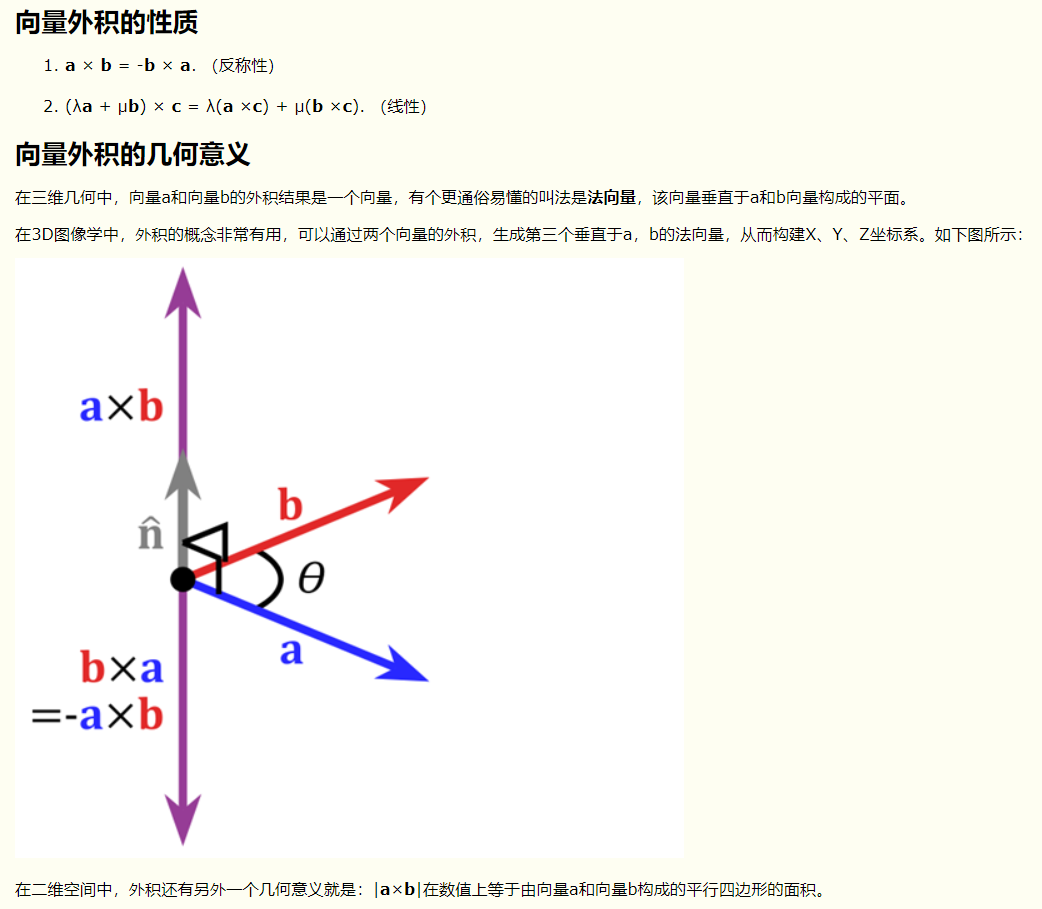
向量的点乘(内积)、叉乘(外积)