High-level idea
- Given a state $s$, the reward $r$ is a function that can tell the agent how good or bad an action $a$ is.
- Based on received rewards, the agent learns to take more good actions and gradually filter out bad actions.
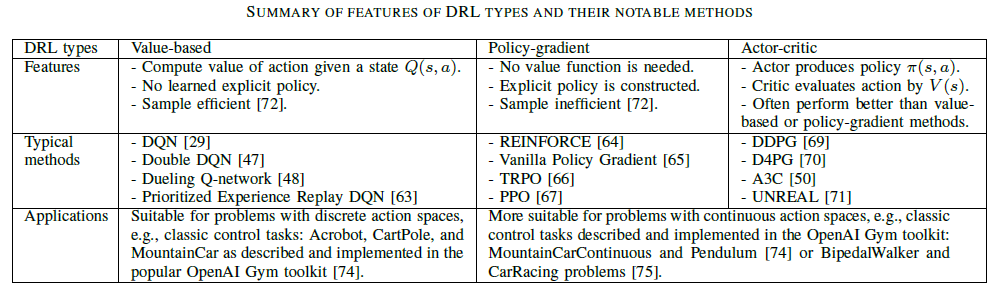
Categorization of methods
- Value-based method: evaluate the goodness of an action given a state using the Q-value function.
- inefficient/impractical when the number of states or actions is large or infinite.
- Policy-gradient method: derive actions directly by learning a policy $\pi(s,a)$ that is a probability distribution over all possible actions.
- suffer from a large fluctuation.
- Actor-critic method (combination of value-based and policy-gradient methods): the actor attempts to learn a policy by receiving feedback from the critic.
- critic-value loss function: $L_1=\sum(R-V(s))^2$, where the discount future reward $R=r+\gamma V(s^\prime)$
- $\gamma \in [0,1]$ is the discount factor that manages the importance levels of future rewards.
- $V(s)$ represents the expected (scalar) reward of a given state
- actor-policy loss function: $L_2=-log(\pi(a \vert s)) * A(s) - \theta H(\pi)$, where the estimated advantage function $A(s)=R-V(s)$
- $H(\pi)$ is the entropy term controlled by the hyperparameter $\theta$.
- $A(s)$ shows how advantageous the agent is when it is in a particular state.
- critic-value loss function: $L_1=\sum(R-V(s))^2$, where the discount future reward $R=r+\gamma V(s^\prime)$