Contents
Time2Graph: Revisiting Time Series Modeling with Dynamic Shapelets

源代码:https://github.com/petecheng/Time2Graph
研究问题
时间序列建模
常用Shapelet(时间序列中最具有辨别性的子序列)方法;每一个Shapelet会在时序中找到最匹配的位置,以及匹配程度。现有工作忽视的问题(以窃电检测为例):
- 出现在不同时间位置的同一个Shapelet可能有不同的含义(冬夏季的低电耗比春季可疑)
- Shapelet的前后演化关系对于全面理解时间序列十分重要(部分正常用户全年耗电量低)
Preliminaries
一个时间序列数据\(t\),可表示为\(n\)个按时间顺序排列的元素\(\{x_1,\cdots ,x_n\}\),则子序列可记作\(s=\{x_i,\cdots ,x_j\}\)。 将\(t\)划分为\(m\)个长度为\(l\)的时间段,则又可记作\(\{s_1, \cdots ,s_m\}=\{\{x_{l*k+1},\cdots ,x_{l*k+l}\}\vert 0\leq k\leq m-1\}\)。
Shapelet与时间序列匹配度的计算
DTW (Dynamic Time Wraping 动态时间规整)
计算两个时间序列的相似度,尤其适用于不同长度、不同节奏的时间序列;warp时间序列(即在时间轴上进行局部的缩放),使得两个序列的形态尽可能的一致,得到最大可能的相似度。
“把序列某个时刻的点跟另一时刻多个连续时刻的点相对应”的做法称为时间规整 (Time Warping)。
对于两个分别长为\(l_1,l_2\)时间序列,规整(对齐)方式\(a=(a_1,a_2)\)是一对长为\(p\)的序号序列。
两个时间序列的距离(不匹配度)定义为
\[d(s_i,s_j)=min_{a\in{A(s_i,s_j)}}\tau(s_i,s_j\vert a)=\tau(s_i,s_j\vert a^*)\]其中\(A(\cdot)\)表示所有可能的规整方式,最优方式记作\(a^*\);\(\tau(\cdot)\)为距离函数,可用欧氏距离。
则shapelet \(v\)和时间序列\(t=\{s_1, \cdots ,s_m\}\)的不匹配度可定义为
\[D(v,t)=min_{1\leq k \leq m}d(v,s_k)\]Shapelet的选取标准
正样本和负样本对于shapelet \(v\)的距离差异尽可能大,即优化损失函数
\[\begin{equation} L=-g(\{D(v,t)\vert t\in T_{pos}\},\{D(v,t)\vert t\in T_{neg}\}) \end{equation}\]其中\(g(\cdot)\)为度量两个集合间差异的函数,可使用信息增益或KL散度;\(T_*\)表示属于某类别的时间序列样本集合。
Time2Graph架构
Time-aware Shapelet
目的:解决相同shapelet出现的不同时间位置对分类的影响。
在选取shapelet用到的损失函数中加入两个可学习的因子:
-
local factor:在计算某shapelet与一个分段的距离(式1)时引入\(w_i\),表示该shapelet中第\(i\)个元素的重要性
\[\hat{d}(v,s\vert w)=\hat{\tau}(v,s\vert a^*,w)=(\sum_{k=1}^pw_{a_1^*(k)}\cdot (v_{a_1^*(k)}-s_{a_2^*(k)})^2)^{\frac{1}{2}}\] -
global factor:在计算shapelet与时间序列的距离(式2)时引入\(u_j\),表示第\(j\)个时间段的重要性
\[\hat{D}(v,t\vert w,u)=min_{1\leq k \leq m}u_k\cdot \hat{d}(v,s_k\vert w)\]
对于每一个候选shapelet \(v\),损失函数(式3)改写为:
\[\hat{L}=-g(\{\hat{D}(v,t)\vert t\in T_{pos}\},\{\hat{D}(v,t)\vert t\in T_{neg}\})+\lambda\vert\vert w\vert\vert + \epsilon\vert\vert u\vert\vert\]最后,选取使得损失函数最小的前K个shapelets。
Shapelet Evolution Graph
目的:考虑shapelet的共现(演化)关系对分类的影响。

图构建算法(Algorithm 1)
-
节点初始化(Ln1):K个shapelets
-
匹配最近shapelets(Ln2~6):对数据集\(T\)中每个时间序列\(t\)的每个时间分段\(s_i\),找到\(N_i\)个距离小于\(\delta\)的shapelet \(v_j\),对应于概率
\[p_{i,j}=\frac{max(\{\hat{d}_{i,k}(v_{i,k},s_i)\vert 1\leq k \leq N_i\})-\hat{d}_{i,j}(v_{i,j},s_i)}{max(\{\hat{d}_{i,k}(v_{i,k},s_i)\vert 1\leq k \leq N_i\})-min(\{\hat{d}_{i,k}(v_{i,k},s_i)\vert 1\leq k \leq N_i\})}\] - 边初始化及权重分配(Ln7~10):对每个相邻时间段\((s_i,s_{i+1})\),遍历共计\(N_i*N_{i+1}\)个最近shapelet组合;对于每个shapelet组合\((v_{i,j},v_{i+1,k})\),增加权重为\(p_{i,j}*p_{i+1,k}\)的有向边\(e_{j,k}\)(重复边合并为一条并累加权重)
- 对于每个顶点,将边权重归一化(Ln12)
Representation learning
首先使用DeepWalk算法生成每个节点的embedding向量;接着,每个时间序列\(t=\{s_1,\cdots,s_m\}\)的embedding使用算法2生成:

- 每个时间分段\(s_i\)的embedding是其对应的最近shapelets组合的加权和(Ln5~7)
- 时间序列\(t\)的embedding则是\(m\)个时间分段embedding的拼接(Ln8)
得到的时间序列表示向量可以用于各种下游分类任务。
实验评估
数据集(3+2):来自UCR-Archive的3个公共数据集,和来自中国国家电网和中国电信的2个真实世界数据集。
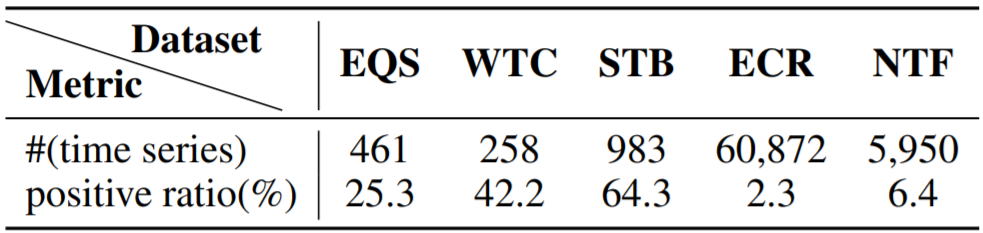
五类Baselines:Distance-based,Feature-based(统计信息),Shapelet-based,Deep-learning-based,Time2Graph变种。
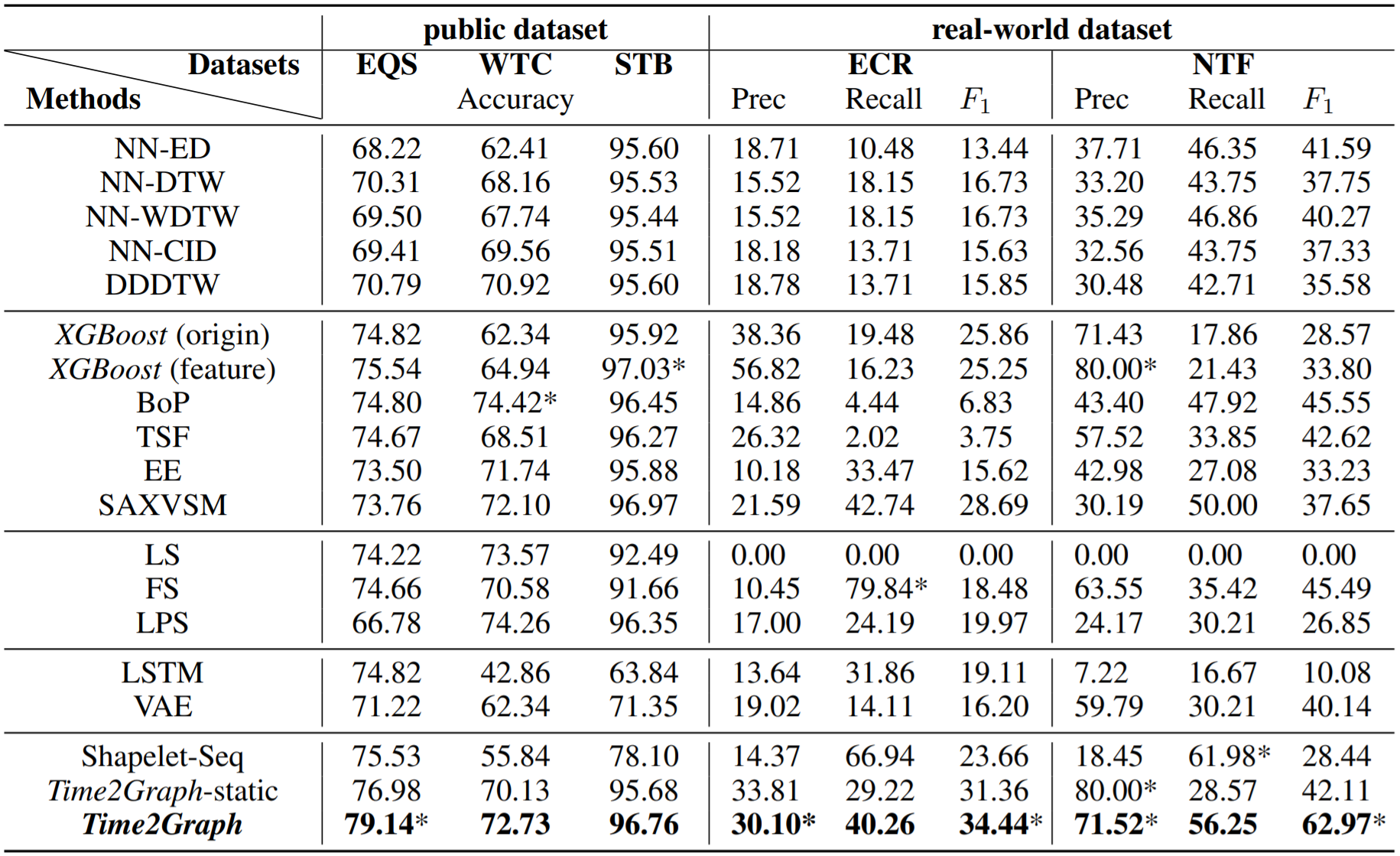
实验结果如下图,其中标(*)的是最优结果。