论文概要
题目:Asm2Vec: Boosting Static Representation Robustness for Binary Clone Search against Code Obfuscation and Compiler Optimization
主要任务:对代码混淆以及编译器优化鲁棒的二进制克隆检测
主要方法:无监督的Assembly Code Representation Learning,学习的对象是汇编代码中的函数(function)的向量表示,顺带还有每个token的。
-
参照NLP中的
PV-DM模型,该模型基于tokens学习文档的表示Doc2Vec。 -
区别:文档是顺序排列的(
sequentially laid out),汇编代码可被视作有特定语法的图(a graph and has a specific syntax)。
PV-DM 模型
论文:Distributed Representations of Sentences and Documents
句向量的分布记忆模型(Distributed Memory version of Paragraph Vectors),同时学习每个词和整个段落的表示(jointly learn vector representations for each word and each paragraph)。
与CBOW模型(Word2Vec)不同的地方在于,输入中多了一个段落的表示向量(paragraph vector)。
在由一系列段落组成的语料库 \(T\) 中,给定一个由多个句子 \(s\) 组成的段落 \(p\) , 在每个句子 \(s\) 上使用一个大小为 \(2k+1\) 的滑动窗口采样,每步向前移动一个单词 \(w\) 。在每一步中,如下图所示:
- 中间一个词作为目标(target),而两边的词作为上下文(context),完成多分类任务。
- 通过段落和词的ID,将它们分别映射到一个对应的向量上。
- 把这些向量加和平均后(经激活函数sigmod),使用多类别分类器(如softmax)预测目标词。
- 分类错误被反向传播,用于更新词和段落向量。
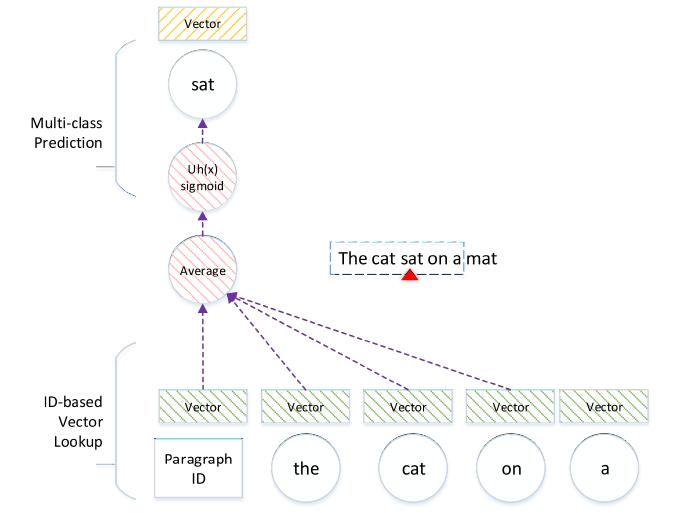
该模型的目标即最大化对数似然概率:
\[\sum_{p}^{T}\sum_{s}^{p}\sum_{t=k}^{\vert{s}\vert-k}logP(w_t\vert{p},w_{t-k},...,w_{t+k}) \tag{1}\]Asm2Vec
Assembly code carries richer syntax than plaintext. It contains operations, operands, and control flow that are structurally different than plaintext.
These differences require a different model architecture design that cannot be addressed by PV-DM. Next, we present a representation learning model that integrates the syntax of assembly code.
CFG序列化
首先有选择地扩展CFG上的callee,然后通过边采样以及随机游走的方法产生汇编代码序列。
-
选择性内联被调用函数
原因:函数内联,即编译器将指定的函数体插入并取代每一处调用该函数的地方(上下文),从而节省了每次调用函数带来的额外时间开支。该优化会很大程度的改变CFG,给汇编克隆搜索带来了很大的挑战。
本文选择满足以下条件的被调用函数进行內联:
- 非库函数。因为模型能较好地获取
library call token的词法语义(lexical semantic)。 - 只內联图上的一阶被调用函数。递归內联会过度扩展caller。
- 沿用 BinGo 的 decoupling metric(式2)和阈值(0.01)。
- caller大于十行指令时,以式3的 \(\delta<0.6\) 过滤太长的被调用函数。caller(\(f_s\))小于十行指令时保留內联,是为了容纳包装函数(
wrapper function)。
- 非库函数。因为模型能较好地获取
-
边采样
从 callee-expanded CFG 上随机采样边,直到每条边都被覆盖。连接每条边前后的汇编代码形成序列。这种做法可以在CFG中的基本块被拆分或合并的情况下,仍能产生相似的序列。
-
随机游走
该方法获得的序列比2中长很多,同时提升了
Dominator的基本块的优先级。(Dominator是控制流分析中的概念:若基本块B向下执行必须经过基本块A,则称A dominates B)
Asm2Vec模型
汇编代码函数库 \(RP\) 中的每个汇编函数 \(f_s\) 由序列集 \(S(f_s)=seq[1:i]\) 表示,一个序列 \(seq_i\) 由一个指令集 \(I(seq_i)=in[1:j]\) 表示。
而一条指令 \(in_j\) 包含一个操作码 \(P(in_j)\) 和一个操作数列表 \(A(in_j)\),将它们连接起来则是标记列表 \(\tau(in_j)=P(in_j)\vert\vert{A(in_j)}\),其中常量被标准化为它们的十六进制形式。
对于每一个指令序列 \(seq_i\) ,以大小为3的滑动窗口向前移动,模型的目标即最大化以下对数似然函数:
\[\sum_{f_s}^{RP}\sum_{seq_i}^{S(f_s)}\sum_{in_j}^{seq_i}\sum_{t_c}^{\tau(in_j)}logP(t_c\vert{p,in_{j-1},in_{j+1}}) \tag{4}\]对应关系:句子 - 序列,词 - 指令;最后多出一个加和,是因为指令可进一步拆分为操作码和操作数
-
每个标识(token)被映射为 \(d\) 维的向量 \(v_t^{\rightarrow}\) ,以及 \(2\times{d}\) 维的映射 \(v_{t'}^{\rightarrow}\)。前者用于生成上下文指令的向量,后者用于(目标指令)标识的预测。
-
每条指令 \(in\) 表示为操作码 \(d\) 维向量与 \(d\) 维操作数向量均值的连接,即 \(2\times{d}\) 维的 \(C\tau{(in)}\) ,如式5所示。
- 每个函数 \(f_s\) 被映射为与指令同维度的 \(2\times{d}\) 维向量,记作 \(\theta_{f_s}^{\rightarrow}\) 。
- \(\theta_{f_s}^{\rightarrow}\) 和 \(v_t^{\rightarrow}\) 的元素初始化为接近0的较小随机值, \(v_{t'}^{\rightarrow}\) 初始化为全0向量。
Training
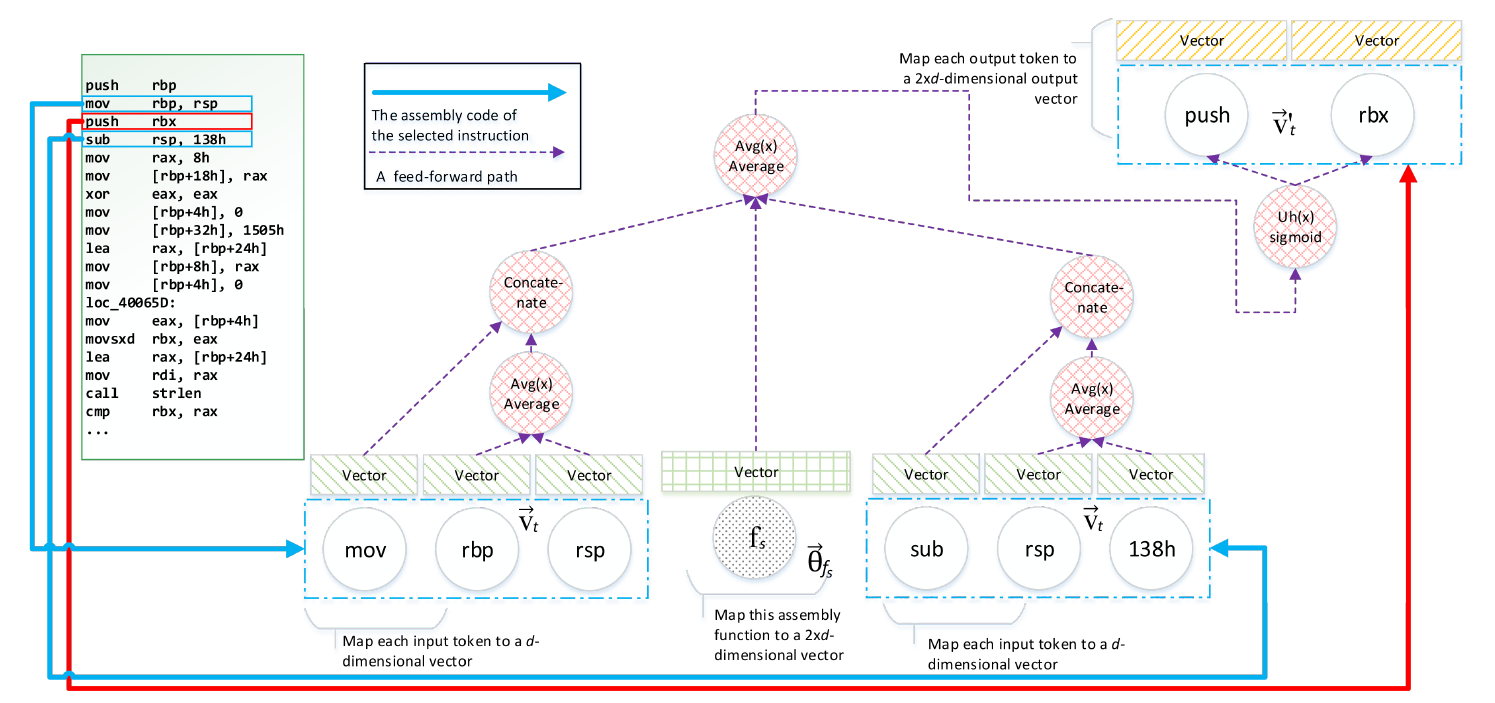
训练时,每一步针对某汇编函数某序列上的一个滑动窗口,输入样本(上下文指令)到其输出(目标指令)的前向传播过程,如图2所示。
\(\theta_{f_s}^{\rightarrow}\) 与目标指令前后两条指令的向量平均后得 \(\delta(in_j,f_s)\) ,则式4中的概率项可表示为 \(P(t_c\vert\delta(in_j,f_s))\) 。
对于目标指令 \(\tau(in_j)\) 中的每一个标识 \(t_c\),查找 \(2\times{d}\) 维的映射 \(v_{t'}^{\rightarrow}\),则上述概率项可建模为softmax多项回归问题:
\[P(t_c\vert\delta(in_j,f_s))=P(v_{t'_c}^{\rightarrow}\vert\delta(in_j,f_s))=\frac{f(v_{t'_c}^{\rightarrow},\delta(in_j,f_s))}{\sum_d^Df(v_{t'_d}^{\rightarrow},\delta(in_j,f_s))} \tag{6}\]其中, \(f(v_{t'_c}^{\rightarrow},\delta(in_j,f_s))=Uh((v_{t'_c}^{\rightarrow})^T\times\delta(in_j,f_s))\), \(Uh\) 为sigmod激活函数。
训练加速
式6中的 \(D\) 表示整个 \(RP\) 中的token词表,因此每次计算softmax涉及的参数量多达 \({(\vert{D}\vert+1)}\times2\times{d}\) 个。故采用k-负样本采样来近似计算,即式6中的分母可表示为:
\[\sum_d^Df(v_{t'_d}^{\rightarrow},\delta(in_j,f_s))\approx{\sum_{i=1}^kE_{d_t\sim{P_n(t_c)}}([t_d\neq{t_c}]f(v_{t'_d}^{\rightarrow},\delta(in_j,f_s)))} \tag{7}\]其中的 \([·]\) 表示恒等函数(identity function:函数参数没有任何限制,参数值永远等于函数值),参数中的表达式为真则为1,否则等于0。其中的 \(E_{d_t\sim{P_n(t_c)}}\) 表示依据负样本分布 \(P_n(t_c)\) 构造的采样函数。
将损失函数分别对 \(\theta_{f_s}^{\rightarrow}\) 和所有涉及到的(上下文指令的token) \(v_t^{\rightarrow}\)以及(目标指令的token) \(v_{t'}^{\rightarrow}\) 求导,再通过反向传播更新向量。
Estimating
在代码克隆的检测任务中,除了通过上述训练步骤获得 \(RP\) 中的汇编函数向量,还需要将一个新的查询(query)函数表示为向量。
此时固定 \(v_t^{\rightarrow}\)和 \(v_{t'}^{\rightarrow}\) ,只需要反向传播更新 \(\theta_{f_s}^{\rightarrow}\) 即可,如算法2所示。

在搜索匹配时,使用余弦相似性。
My Review
本文使用的表征学习并非神经网络更新权重的方法,其输入到输出的关系是固定的(简单的加和与非线性),更新的是token和function的特征向量。
式6中f的计算要求token向量是 \(2\times{d}\) 维的,因此需要一个该维度的映射。个人感觉token两种维度embedding的设计有点牵强。
为什么不按如下方法(式8)优化?更加直接:
\[\sum_{f_s}^{RP}\sum_{seq_i}^{S(f_s)}\sum_{in_j}^{seq_i}logP(in_j\vert{p,in_{j-1},in_{j+1}}) \tag{8}\]其中的概率项 \(P(in_j\vert\delta(in_j,f_s))=P(C\tau{(in_j)}\vert\delta(in_j,f_s))\)
