Evaluating Explanation Without Ground Truth in Interpretable Machine Learning

arXiv’19, cite:24, PDF link: https://arxiv.org/pdf/1907.06831.pdf

F Yang, Texas A&M University(美国，得州农工大学)

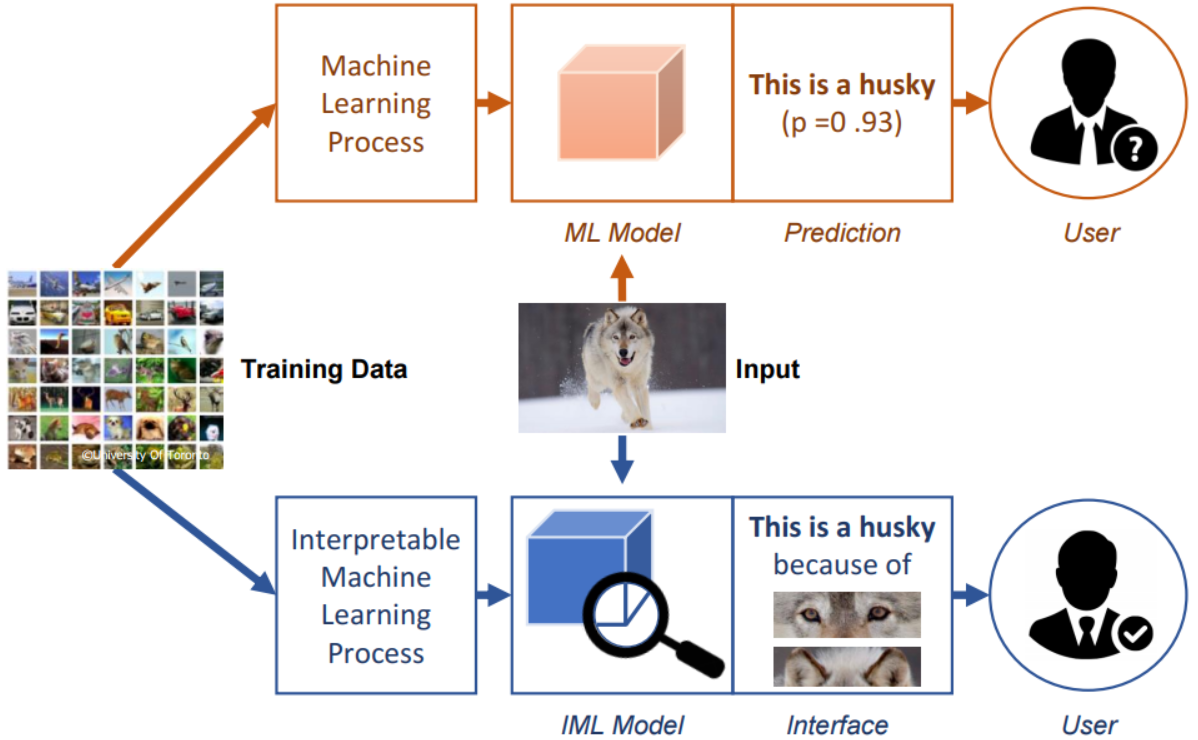
Interpretable Machine Learning (IML)

• Aiming to help humans understand the machine learning decisions.
• IML model is capable of providing specific reasons for particular machine decisions, while ML model may simply provide the prediction results with probability scores.

A two-dimensional categorization

• Scope dimension
  • global: the overall working mechanism of models -> interpret structures or parameters
  • local: the particular model behavior for individual instance -> analyze specific decisions
• Manner dimension
  • intrinsic: achieved by self-interpretable models
  • post-hoc (also written as posthoc): requires another independent interpretation model or technique

上半年在实习没有更博，做了与手机指纹认证相关的项目，由于项目需要阅读了 AOSP 相应部分的源码，在这篇博文里做一个系统化的整理~

安卓生物识别架构

Android Q(10) 开始引入了 BiometricManager 类，本文基于这一架构，结合最新的 AOSP 源码介绍安卓的指纹识别架构，侧重与发起指纹认证相关的方法（非其它生物认证方式或录入流程）。

Android Code Search: https://cs.android.com/

BiometricManager

frameworks/base/core/java/android/hardware/biometrics/BiometricManager.java

/**
 * A class that contains biometric utilities. For authentication, see {@link BiometricPrompt}.
 */

• static final 成员变量：定义在 BiometricConstants 类中的 SUCCESS, ERROR_HW_UNAVAILABLE, ERROR_NONE_ENROLLED, NO_HARDWARE

• 构造函数：传入 Context, IAuthService (Communication channel from BiometricPrompt and BiometricManager to AuthService)

  AuthService: System service that provides an interface for authenticating with biometrics and PIN/pattern/password to BiometricPrompt and lock screen.

  在系统层，根据认证类型注册相应的服务（FingerprintService, FaceService, IrisService），做检查权限等

• 接口 Authenticators：认证类型的结合(e.g. DEVICE_CREDENTIAL | BIOMETRIC_WEAK)，包含生物认证的强度（STRONG, WEAK），用于设备保护的非生物认证方式（DEVICE_CREDENTIAL: PIN, pattern, password）

• canAuthenticate, hasEnrolledBiometrics 方法：检查设备是否支持生物识别身份验证，是否有录入的生物特征，以及相应的权限检查

论文 DeepReflect: Discovering Malicious Functionality through Binary Reconstruction 被 USENIX Security ‘21 (Fall) 录用，来自佐治亚理工的 Wenke Lee 团队：

源码地址：https://github.com/evandowning/deepreflect

Motivation：恶意应用分析师的故事

Molly 是一名恶意应用分析师，她每天的主要任务就是理解恶意样本并给出技术报告。当拿到一个恶意样本时，Molly 有着一套如 图1 所示的工作流程，她首先将样本上传到 VirusTotal 等平台扫描，如果是一个已被恶意样本库收录的应用，她就可以轻松地结束本次工作。但这样的好事并不多见，因为待分析的往往是公司恶检系统的漏网之鱼。接着，她选择使用定制的沙箱来运行样本，以动态分析应用的恶意行为，但狡猾的样本采用了沙箱逃逸技术（检测到沙箱环境时则不执行部分代码）。于是，她又使用了一些内部工具，企图哄骗应用去执行隐藏的行为，却都无济于事。无奈之下，她只能将应用解包（脱壳）后做静态分析。