B-样条基函数
最简单的B样条基函数是由de Boor-Cox递推公式定义的:
\[N_{i,0}(t) = \left\{\begin{matrix} 1 & t_i < t< t_{i+1}\\ 0 & otherwise \end{matrix}\right.\\ N_{i,k} = \frac{t - t_i}{t_{i+k} - t_{i}}N_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i+k+1} - t_{i+1}} N_{i+1,k-1}(t)\]其中\(t\)为节点向量,非减的实数序列:
\[t_0,t_1,...,t_{k-1},t_k,...,t_n,t_{n+1},...,t_{n+k-1},t_{n+k+1}.\]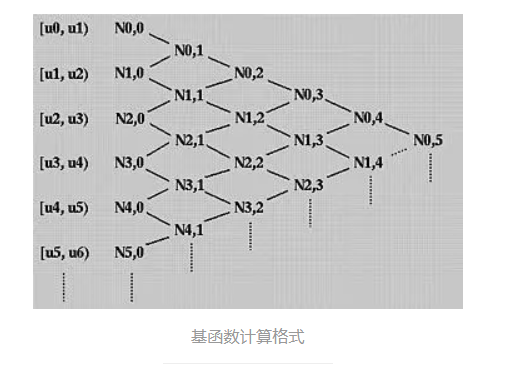
加深理解:基函数的非零区间?节点个数?

重要性质
-
局部支撑性 (Local Support)
\(N_{i,k}(t)\)是非负的,\(N_{i,k}(t)\)是\([t_i,t_{i+k+1}]\)上的分段非零多项式:
\[N_{i,k}(t) = \left \{ \begin{matrix} \ge 0 & t\in [t_i,t_{i+k+1}]\\ =0& otherwise \end{matrix} \right.\] -
归一性 区间\([t_i,t_{i+1}]\)上的所有\(k\)次非零基函数的和为1:
\[\sum_{i=0}^n N_{i,k}(t) = 1,t \in [t_i,t_{i+1}].\]
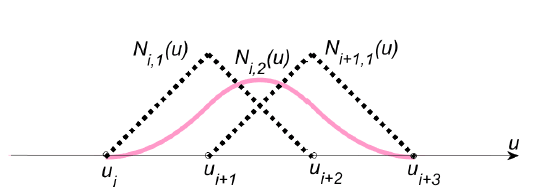
下图也展示了在函数定义域上的一个区间内只有k+1个基函数非0:
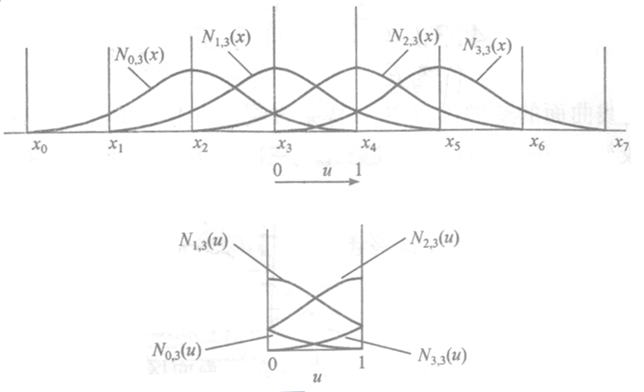
B-样条曲线
给定\(n+1\)个控制点\({P_0,P_1,…,P_n}\),\(m+1\)个节点\(\{u_0,u_1,…,u_m\}\), \(p\)阶B样条曲线的定义是:
\[C(u)=\sum_{i=0}^{n}N_{i,p}(u)P_i\]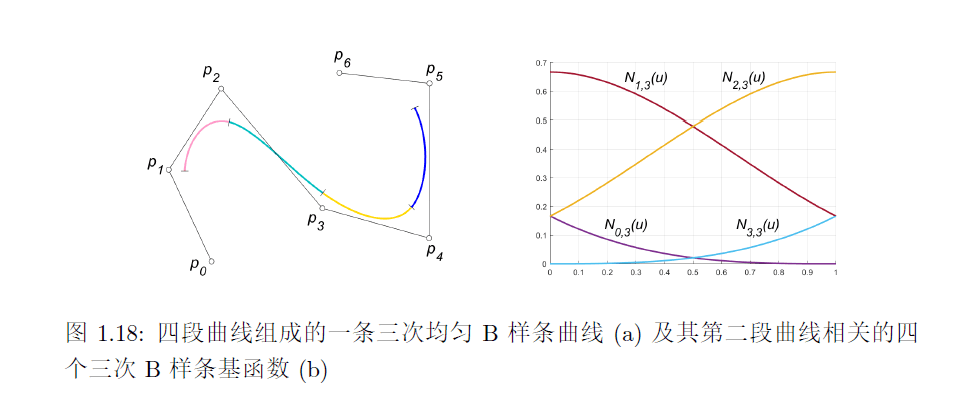
对比Bezier曲线
相对Bezier曲线不同之处
- B样条的控制点个数与曲线次数无关,因此B样条的自由度更大,可以定义很多控制点又不用担心曲线次数过高而计算困难。
- B样条有多个节点区间,使得其为分段函数,而Bezier曲线只有一个区间。
与Bezier曲线的联系
- B样条上任意一个区间\([ui,ui+1)\)上的曲线的定义都是一个Bezier。因此可以将B样条转为分段bezier曲线。
- Bezier是一种特殊的样条曲线。
三种类型:open, clamped, closed
-
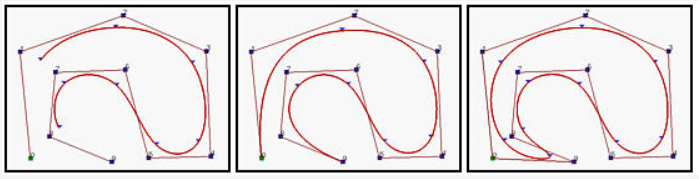
open: 如果节点向量没有任何特别的结构,那么产生的曲线不会与控制折线(polyline)的第一边(leg)和最后一边(leg)接触,如下面左图所示。
-
clamped: 我们可能想强制曲线使得它分别与第一个控制点和最后一个控制点的第一边和最后一边相切,像贝塞尔曲线那样。为了做到这些,第一个节点和最后一个节点必须是重复度为p+1。参见下边中间的图。
Clamped列表(3阶为例):前面3+1个参数均设置为0,后面3+1个参数均设置为1,然后剩余参数均匀递增:0,0,0,0,1/3,2/3,1,1,1,1
-
closed: 通过重复某些节点和控制点,产生的曲线的开始和结尾连接在一起形成了一个闭环,如下边右图所示。
生成闭曲线
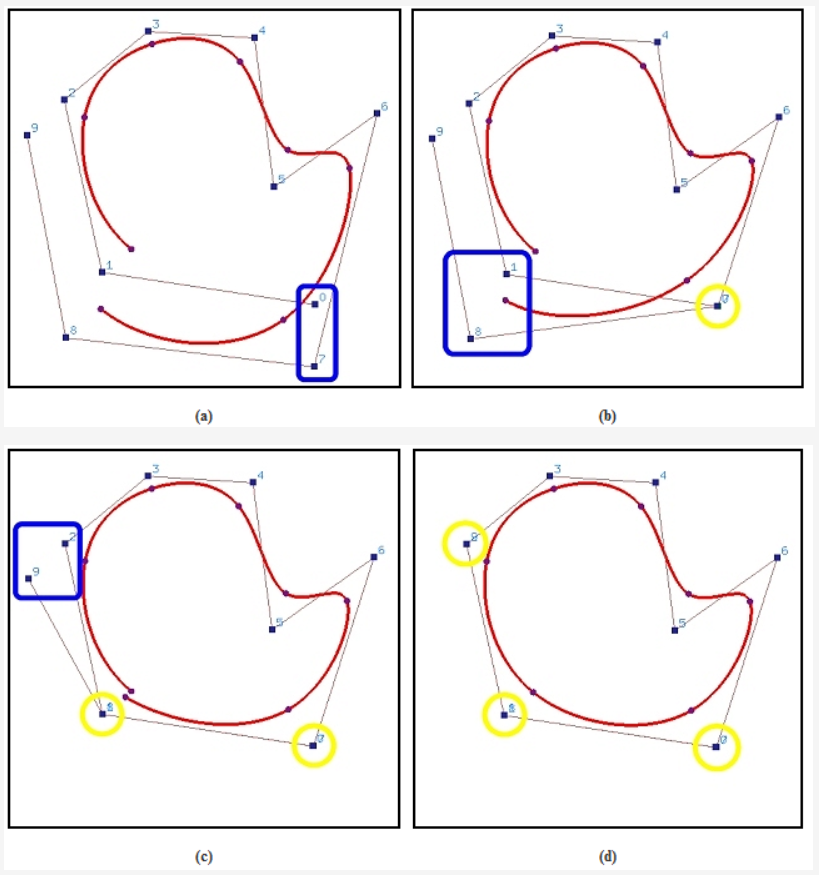
简单的方法有Wrapping控制点或者Wrapping节点,下图为前者的例子:
图 (a) 显示了一个由10(n=9)个控制点和一个均匀节点向量定义的3次开(open)B-样条曲线。在图中,控制点对0 和7, 1和8, 以及2和9放置在相互靠近的地方来说明这个构建。图 (b) 显示了使得点0和7重叠的结果。 曲线的形状没有太大变化。那么,控制点1和8重叠如图(c)所示。很显然曲线的第一点和最后一点的间距更近了。最后曲线变成一个闭曲线当控制点2和9重叠后,如图(d)所示。
B-样条曲面
给定控制点\(P_{ij}\)以及\(U,V\)轴上的节点向量:
\[U = [u_0,u_1,...,u_{m+p}]\\ V = [v_0,v_1,...,v_{n+q}]\]阶为\(p×q\)的B-样条曲面可以定义为:
\[P(u,v) = \sum_{i=0}^m \sum_{j=0}^n P_{ij}N_{i,p}(u)N_{j,q}(v)\]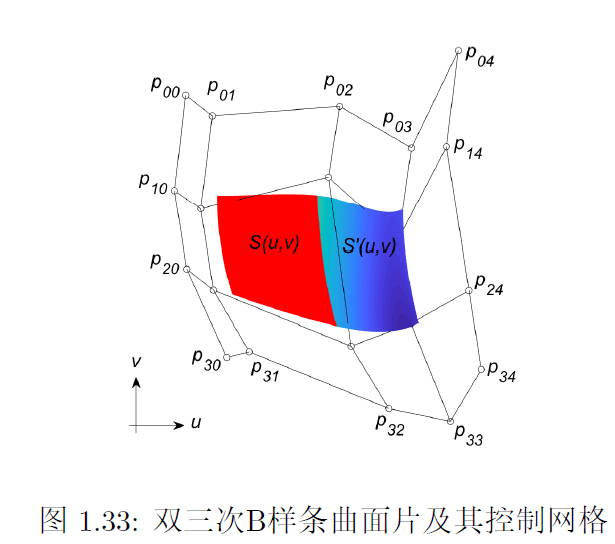
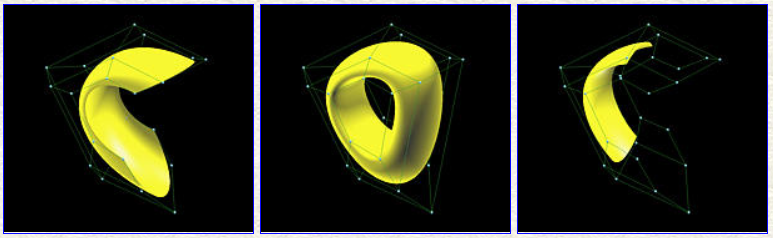
三种类型:open, clamped, closed
The following figures show three B-spline surfaces clamped, closed and open in both directions. All three surfaces are defined on the same set of control points; but, as in B-spline curves, their knot vectors are different.
参考资料
