Contents
How Powerful are Graph Neural Networks?

预备知识
GNN
注:下表中GCN一行的公式包含了AGGREGATE和COMBINE两步。
| AGGREGATE | COMBINE | |
|---|---|---|
| GraphSAGE | \(a_v^{(k)}=MAX(\{ReLU(W\cdot{h_v^{(k-1)}),\forall{u\in}N(v)\}})\) | \(W\cdot{[h_v^{(k-1)},a_v^{(k)}]}\) |
| GCN(2017第四代) | \(h_v^{(k)}=ReLU(W\cdot{MEAN\{h_v^{(k-1)},\forall{u\in}N(v)\bigcup{\{v\}}\}})\) |
GCN的公式为什么可以理解为求平均?
\[H^{l+1}=\sigma(\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})\\ =\sigma(\hat{A}H^{(l)}W^{(l)})\]参考资料:1. GraphSAGE:我寻思GCN也没我牛逼,2. 一文读懂图卷积GCN
-
\(\hat{A}\): 邻接矩阵A的归一化

-
\(\hat{A}\cdot{H}\)的含义:
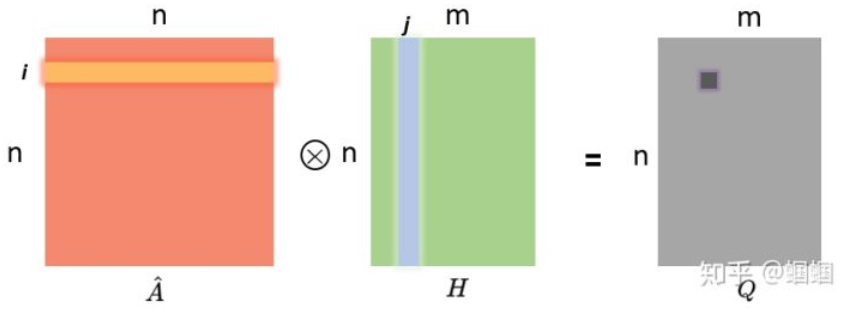
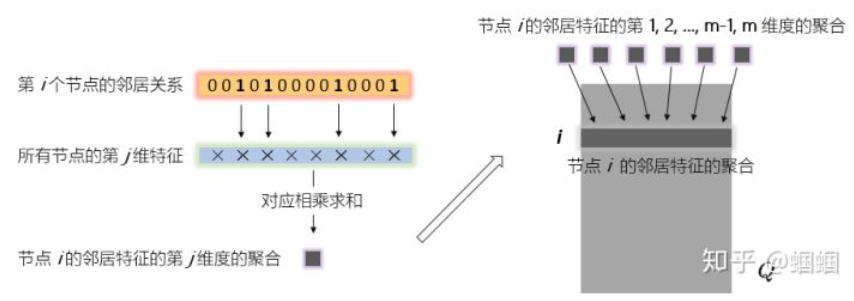
GCN聚合的理解
WL test
解决图同构问题,即两个图的拓扑结构是否相同。
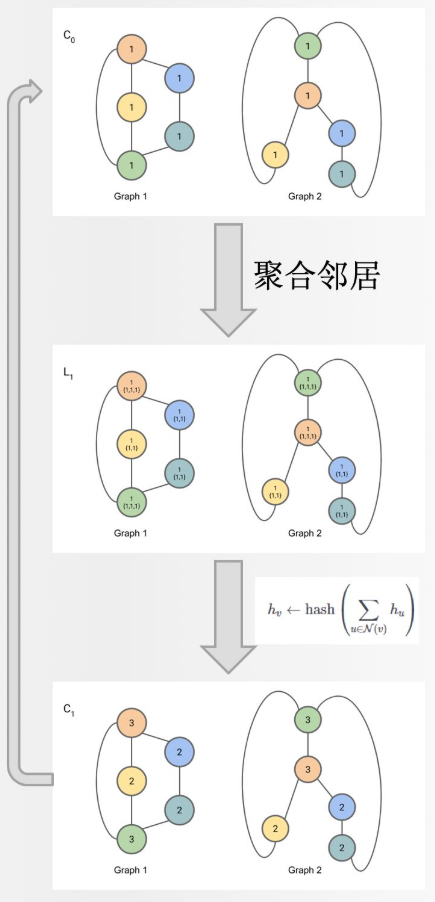
给定两个Graph,算法流程即迭代以下两步:
(1) 聚合各节点及其邻居节点的标签
(2) 将聚合后的标签哈希到一个唯一的新标签
若在某一轮迭代中,两个Graph的节点标签出现了不一致的情况,则不同构。
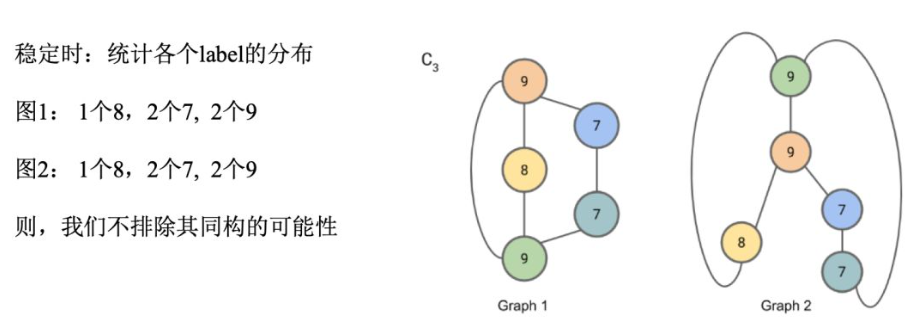
理论架构
- 建模邻居节点集合为多重集(Multiset,即元素可以重复出现的集合),原因是不同的节点可能具有相同的特征向量;
- 最强的GNN仅仅在两个节点具有特征相同的子树(subtree)时,才将它们映射到同一位置。
问题转化:GNN的聚合方案是不是单射(injective)的多重集函数?
构建图神经网络
引理2
在图同构问题中,WL test是GNN的能力上限。
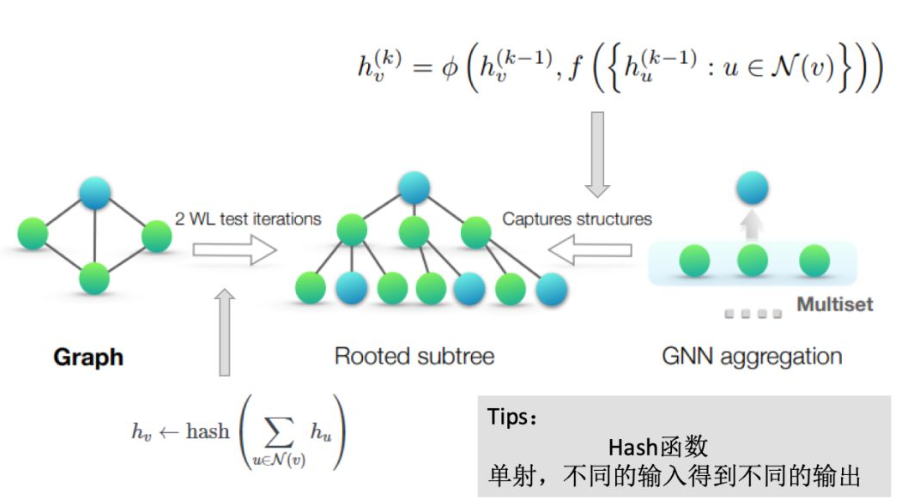
定理3
满足以下两个条件的GNN可以达到WL test的能力:
- 对于聚合方案\(h_v^{(k)}=\phi(h_v^{(k-1)},f(\{h_u^{(k-1)},\forall{u\in}N(v)\}))\),多重集函数\(f\)以及函数\(\phi\)是单射的;
- Graph-level的READOUT方法是单射的。
引理4
假定输入的节点特征空间\(\mathcal{X}\)可数,设\(g^{(k)}\)是GNN第k层的参数方程,其中\(g(1)\)是定义在有边界大小的多重集\(X\in\mathcal{X}\)上的。\(g^{(k)}\)的范围,即隐藏层的节点特征\(h_v^{(k)}\)的空间也是可数的。
GNN较WL的优势之一:将相似的图结构映射到相近的位置,而WL是one-hot的
GIN
引理5 (加和聚合SUM可以表示单射)
假定\(\mathcal{X}\)可数,则存在函数\(f:\mathcal{X}\rightarrow R^n\)使得对于每个有边界大小的多重集\(X\in\mathcal X\)而言,\(h(X)=\sum_{x\in{X}}f(x)\)是唯一的。则任意多重集函数\(g\)可以被分解为\(g(X)=\phi(\sum_{x\in{X}}f(x))\),其中\(\phi\)为某种函数。
推论6
对于\(c\in\mathcal{X},X\in\mathcal{X}\)的每一对\((c,X)\),存在函数\(f:\mathcal{X}\rightarrow R^n\)使得\(h(c,X)=(1+\epsilon)\cdot{f(c)}+\sum_{x\in{X}}f(x)\)都是唯一的,其中\(\epsilon\)有包括无理数在内的无穷种选择。则函数\(g\)又可以被分解为\(g(c,X)=\varphi((1+\epsilon)\cdot{f(c)}+\sum_{x\in{X}}f(x))\),其中\(\varphi\)为某种函数。
因此,可以使用多层感知机(MLPs)来建模学习推论中的函数\(f\)和\(\varphi\)。
-
由于MLPs可以表示函数的组合,所以用一个MLP来表示\(f^{(k+1)}\circ \varphi^{(k)}\)。
-
在第一次迭代中,如果输入特征是独热编码则不需要在加和之前使用MLPs,因为它们的加和本身就是单射的。
-
参数\(\varphi\)可以设置为一个可学习的参数或者固定的标量。
综上,GIN更新节点表示的公式为:
\[h_v^{(k)}=MLP^{(k)}((1+\epsilon^{(k)})\cdot h_v^{(k-1)}+\sum_{u\in{N(v)}}h_u^{(k-1)})\]GIN仅是maximally powerful GNN的一种实现,优点是形式简单。
READOUT
使用了模型每次迭代后的信息:
\[h_G=CONCAT(READOUT({h_v^{(k)}\vert v\in G})\vert k=0,1,...,K)\]A sufficient number of iterations is key to achieving good discriminative power. Yet, features from earlier iterations may sometimes generalize better.
根据定理3和推论6,如果GIN用加和表示上式中的READOUT,则可证明地推广了WL test。
其它GNN模型
-
引理7 单层感知机是不够的
-
MEAN和MAX的局限性
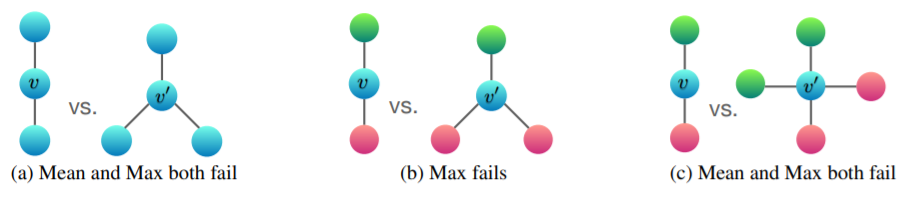
但是MEAN学习了分布,MAX学习了显著值
实验
(1) 训练集表现
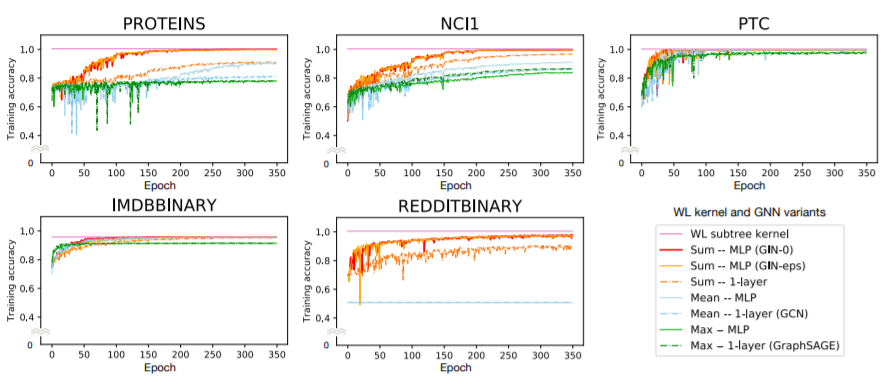
(2) 测试集表现
-
State-of-the-art Baseline
-
(1) the WL subtree kernel (Shervashidze et al., 2011)
C-SVM (Chang & Lin, 2011) was used as a classifier; the hyper-parameters we tune are C of the SVM and the number of WL iterations ∈ {1, 2, . . . , 6};
-
(2) state-of-the-art deep learning architectures, i.e.,
- Diffusion convolutional neural networks (DCNN) (Atwood & Towsley, 2016)
- PATCHY-SAN (Niepert et al., 2016)
- Deep Graph CNN (DGCNN) (Zhang et al., 2018);
-
(3) Anonymous Walk Embeddings (AWL) (Ivanov & Burnaev, 2018).
-
For the deep learning methods and AWL, we report the accuracies reported in the original papers.
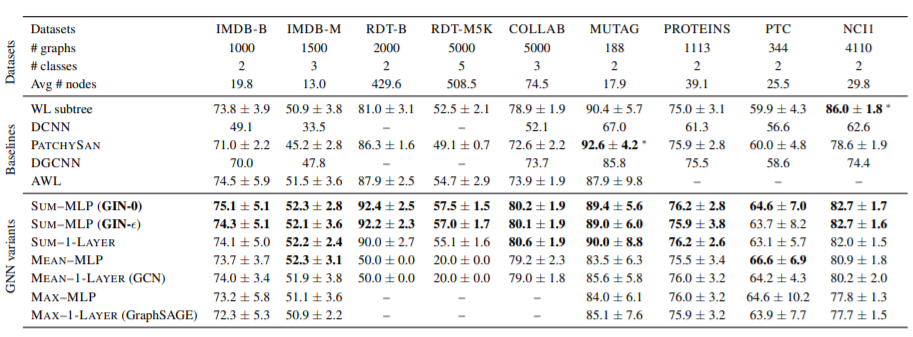
- 数据集备注
- 前五个数据集:社交网络,后四个:生物信息
- 节点特征:社交网络数据集中,RDT是置为相同的,另外三个为节点的度。
- GIN-0 在训练集上表现相当,但在测试集上始终比 GIN-\(\epsilon\) 优一点
