论文代码
首先分析一下作者的源码。
ExplainModule这个类定义了GNNExplainer网络的模块结构,继承自nn.Module:
init时用construct_edge_mask和construct_feat_mask函数初始化要学习的两个mask(分别对应于两个nn.Parameter类型的变量:\(n\times n\)维的mask,\(d\)维全0的feat_mask);diag_mask即主对角线上是0,其余元素均为1的矩阵,用于_masked_adj函数。
_masked_adj函数将mask用sigmod或ReLu激活后,加上自身转置再除以2,以转为对称矩阵,然后乘上diag_mask,最终将原邻接矩阵adj变换为masked_adj。
下面分析一下其中的forward和loss函数。
前向传播
这里首先是把待学习的参数mask和feat_mask分别乘原邻接矩阵和特征向量,得到变换后的masked_adj和x。前者通过调用_masked_adj函数完成,后者的实现如下:
feat_mask = (
torch.sigmoid(self.feat_mask)
if self.use_sigmoid
else self.feat_mask
)
if marginalize:
std_tensor = torch.ones_like(x, dtype=torch.float) / 2
mean_tensor = torch.zeros_like(x, dtype=torch.float) - x
z = torch.normal(mean=mean_tensor, std=std_tensor)
x = x + z * (1 - feat_mask)
else:
x = x * feat_mask
这里需说明的是marginalize为True的情况,参见论文4.2节的Learning binary feature selector F:
-
如果同
mask一样学习feature_mask,在某些情况下会导致重要特征也被忽略(学到的特征遮罩也是接近于0的值),因此依据\(X_S\)的经验边缘分布使用蒙特卡罗方法来抽样得\(X=X^F_S\)。 -
为了解决随机变量\(X\)反向传播的问题,引入了“重参数化”的技巧,即将其表示为一个无参的随机变量\(Z\)的确定性变换:
\[X=Z+(X_S-Z)\bigodot F \\s.t.\sum_j F_j\leq K_F\]其中,\(Z\)是依据经验分布采样得到的\(d\)维随机变量,\(K_F\)是表示保留的最大特征数的参数(
utils/io_utils.py中的denoise_graph函数)。
接着将masked_adj和x输入原始模型得到ExplainModule结果pred。
损失函数
五项损失的加权,除了对应于论文中损失函数公式的pred_loss,其余各项损失的作用参考论文4.2节的Integrating additional constraints into explanations,它们的权重定义在coeffs中:
self.coeffs = {
"size": 0.005,
"feat_size": 1.0,
"ent": 1.0,
# "feat_ent": 0.1,
# "grad": 0,
"lap": 1.0,
}
use element-wise entropy to encourage structural and node feature masks to be discrete;
penalize large size of the explanation by adding the sum of all elements of the mask paramters;
can encode domain-specific constraints through techniques like Lagrange multiplier of constraints or additional regularization terms.
-
pred_loss
\[\mathop{min}\limits_{M,F}-\sum_{c=1}^C \mathbb l[y=c]logP_{\phi}(Y=y\vert G=G_S,X=X_S^F)\]mi_obj = False if mi_obj: pred_loss = -torch.sum(pred * torch.log(pred)) else: pred_label_node = pred_label if self.graph_mode else pred_label[node_idx] gt_label_node = self.label if self.graph_mode else self.label[0][node_idx] logit = pred[gt_label_node] pred_loss = -torch.log(logit)其中
pred是当前的预测结果,pred_label是原始特征上的预测结果。 -
mask_ent_loss
mask_ent = -mask * torch.log(mask) - (1 - mask) * torch.log(1 - mask) mask_ent_loss = self.coeffs["ent"] * torch.mean(mask_ent) -
size_loss
# size mask = self.mask if self.mask_act == "sigmoid": mask = torch.sigmoid(self.mask) elif self.mask_act == "ReLU": mask = nn.ReLU()(self.mask) size_loss = self.coeffs["size"] * torch.sum(mask) -
feat_size_loss
feat_mask = ( torch.sigmoid(self.feat_mask) if self.use_sigmoid else self.feat_mask ) feat_size_loss = self.coeffs["feat_size"] * torch.mean(feat_mask) -
lap_loss
D = torch.diag(torch.sum(self.masked_adj[0], 0)) m_adj = self.masked_adj if self.graph_mode else self.masked_adj[self.graph_idx] L = D - m_adj pred_label_t = torch.tensor(pred_label, dtype=torch.float) if self.args.gpu: pred_label_t = pred_label_t.cuda() L = L.cuda() if self.graph_mode: lap_loss = 0 else: lap_loss = (self.coeffs["lap"] * (pred_label_t @ L @ pred_label_t) / self.adj.numel() )
关于源码中feat_mask_ent_loss(乘了feat_ent权重的那项)为什么没有加进去,RexYing给我的回复:
mask_ent = -mask * torch.log(mask) - (1 - mask) * torch.log(1 - mask)
mask_ent_loss = self.coeffs["ent"] * torch.mean(mask_ent)
feat_mask_ent = - feat_mask \
* torch.log(feat_mask) \
- (1 - feat_mask) \
* torch.log(1 - feat_mask)
feat_mask_ent_loss = self.coeffs["feat_ent"] * torch.mean(feat_mask_ent)
The mask entropy loss can be added to the final loss to encourage the discreteness of the learned mask. It could be added (e.g. in syn5) to make it easier to threshold the masks (since the mask values are more extreme - close to 0 or close to 1). But I didn’t add it by default, since many tasks work well without the loss.
Explainer这个类实现了解释的逻辑,主函数是其中的explain,用于解释原模型在单节点的预测结果,主要步骤:
- 取子图的
adj,x,label。图解释:取graph_idx对应的整个计算图,节点解释:调用extract_neighborhood函数取该节点num_gc_layers阶数的邻居。 - 将传入的模型预测输出
pred转为pred_label。 - 构建
ExplainModule,进行num_epochs轮训练(前向+反向传播)
explain_nodes、explain_nodes_gnn_stats、explain_graphs这三个函数都是在它的基础上实现的。
PyG实现
为了兼容GNNExplainer,在torch_geometric/nn/conv/message_passing.py中给MessagePassing类增加了__explain__和__edge_mask__属性,并直接在message passing过程中注入edge_mask,此时无法将其和aggregate融合在(为节约时间和内存而设计的)message_and_aggregate函数中完成:
# For `GNNExplainer`, we require a separate message and aggregate
# procedure since this allows us to inject the `edge_mask` into the
# message passing computation scheme.
if self.__explain__:
edge_mask = self.__edge_mask__.sigmoid()
# Some ops add self-loops to `edge_index`. We need to do the
# same for `edge_mask` (but do not train those).
if out.size(0) != edge_mask.size(0):
loop = edge_mask.new_ones(size[0])
edge_mask = torch.cat([edge_mask, loop], dim=0)
assert out.size(0) == edge_mask.size(0)
out = out * edge_mask.view(-1, 1)
这里主要是了解下那两个属性的作用,在阅读源码时不要被困惑了;该函数基类中仅raise NotImplementedError,依赖于派生类自己实现
节点分类解释
在PyG 1.5的版本中已实现,不过对比源码之后发现一些小的不同,这里记录一下:
- 没有将edge_mask处理为对称矩阵的步骤,支持有向图
- 损失函数中的附加项只包含与size和element-wise entropy相关的那四个(系数沿用)
- node_feat_mask没有marginalize,直接用它乘的x(对应论文源码里else的情况)
原先安装了1.4可以使用以下命令升级:
$ conda install pytorch torchvision cudatoolkit=10.1 -c pytorch
# ${CUDA}:根据Pytorch的安装选择cpu, cu92, cu100, cu101,如这里是cu101
$ pip install torch-scatter==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.5.0.html
$ pip install torch-sparse==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.5.0.html
$ pip install torch-cluster==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.5.0.html
$ pip install torch-spline-conv==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.5.0.html
$ pip install torch-geometric --upgrade
参考官方示例,首先通过Planetoid类下载Cora数据集(文献引用网络),训练一个两层GCN模型:
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.lin = Sequential(Linear(10, 10))
self.conv1 = GCNConv(dataset.num_features, 16)
self.conv2 = GCNConv(16, dataset.num_classes)
def forward(self, x, edge_index):
x = F.relu(self.conv1(x, edge_index))
x = F.dropout(x, training=self.training)
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
"""Planetoid:
The citation network datasets "Cora", "CiteSeer" and "PubMed" from the
`"Revisiting Semi-Supervised Learning with Graph Embeddings"
<https://arxiv.org/abs/1603.08861>`_ paper.
Nodes represent documents and edges represent citation links.
Training, validation and test splits are given by binary masks.
"""
dataset = 'Cora'
path = osp.join(osp.dirname(osp.abspath('')), '..', 'data', 'Planetoid')
dataset = Planetoid(path, dataset, transform=T.NormalizeFeatures())
data = dataset[0]
随后将模型和待解释的节点ID输入,训练GNNExplainer:
explainer = GNNExplainer(model, epochs=200)
node_idx = 10
node_feat_mask, edge_mask = explainer.explain_node(node_idx, x, edge_index)
最后可以用explainer的visualize_subgraph方法来可视化:
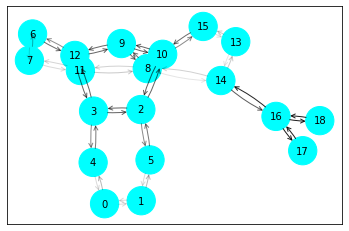
ax, G = explainer.visualize_subgraph(node_idx, edge_index, edge_mask, y=data.y)
plt.show()
结果如下图所示,节点10即待解释的节点,其计算图包含了两跳节点,因为模型使用了两个GCN卷积层,参考源码中的__num_hops__函数。其中节点的颜色表示其类别,黑色边连接起来的计算图对预测节点10的标签来说是重要的,即论文中的\(G_S\)。
图分类解释
PyG中尚未实现,但根据论文的4.4节,只要把损失函数中节点计算图的邻接矩阵\(A_c\)替换成待解释图上全部节点的邻接矩阵即可,代码中主要不同点有:
- 要学习的Mask作用在整个图上,不用取子图
- 标签预测和损失函数的对象是单个graph
实现代码如下,这里我默认不学习node_feat_mask,要学习的话需在初始化GNNExplainer时将node置为True。
from math import sqrt
import torch
from tqdm import tqdm
import matplotlib.pyplot as plt
import networkx as nx
from torch_geometric.nn import MessagePassing
from torch_geometric.data import Data
from torch_geometric.utils import k_hop_subgraph, to_networkx
import numpy as np
EPS = 1e-15
class GNNExplainer(torch.nn.Module):
r"""
Args:
model (torch.nn.Module): The GNN module to explain.
epochs (int, optional): The number of epochs to train.
(default: :obj:`100`)
lr (float, optional): The learning rate to apply.
(default: :obj:`0.01`)
log (bool, optional): If set to :obj:`False`, will not log any learning
progress. (default: :obj:`True`)
"""
coeffs = {
'edge_size': 0.001,
'node_feat_size': 1.0,
'edge_ent': 1.0,
'node_feat_ent': 0.1,
}
def __init__(self, model, epochs=100, lr=0.01, log=True, node=False): # disable node_feat_mask by default
super(GNNExplainer, self).__init__()
self.model = model
self.epochs = epochs
self.lr = lr
self.log = log
self.node = node
def __set_masks__(self, x, edge_index, init="normal"):
(N, F), E = x.size(), edge_index.size(1)
std = 0.1
if self.node:
self.node_feat_mask = torch.nn.Parameter(torch.randn(F) * 0.1)
std = torch.nn.init.calculate_gain('relu') * sqrt(2.0 / (2 * N))
self.edge_mask = torch.nn.Parameter(torch.randn(E) * std)
self.edge_mask = torch.nn.Parameter(torch.zeros(E)*50)
for module in self.model.modules():
if isinstance(module, MessagePassing):
module.__explain__ = True
module.__edge_mask__ = self.edge_mask
def __clear_masks__(self):
for module in self.model.modules():
if isinstance(module, MessagePassing):
module.__explain__ = False
module.__edge_mask__ = None
if self.node:
self.node_feat_masks = None
self.edge_mask = None
def __num_hops__(self):
num_hops = 0
for module in self.model.modules():
if isinstance(module, MessagePassing):
num_hops += 1
return num_hops
def __flow__(self):
for module in self.model.modules():
if isinstance(module, MessagePassing):
return module.flow
return 'source_to_target'
def __subgraph__(self, node_idx, x, edge_index, **kwargs):
num_nodes, num_edges = x.size(0), edge_index.size(1)
if node_idx is not None:
subset, edge_index, mapping, edge_mask = k_hop_subgraph(
node_idx, self.__num_hops__(), edge_index, relabel_nodes=True,
num_nodes=num_nodes, flow=self.__flow__())
x = x[subset]
else:
x=x
edge_index=edge_index
row, col = edge_index
edge_mask = row.new_empty(row.size(0), dtype=torch.bool)
edge_mask[:]=True
mapping = None
for key, item in kwargs:
if torch.is_tensor(item) and item.size(0) == num_nodes:
item = item[subset]
elif torch.is_tensor(item) and item.size(0) == num_edges:
item = item[edge_mask]
kwargs[key] = item
return x, edge_index, mapping, edge_mask, kwargs
def __graph_loss__(self, log_logits, pred_label):
loss = -torch.log(log_logits[0,pred_label])
m = self.edge_mask.sigmoid()
loss = loss + self.coeffs['edge_size'] * m.sum()
ent = -m * torch.log(m + EPS) - (1 - m) * torch.log(1 - m+ EPS)
loss = loss + self.coeffs['edge_ent'] * ent.mean()
return loss
def visualize_subgraph(self, node_idx, edge_index, edge_mask, y=None,
threshold=None, **kwargs):
r"""Visualizes the subgraph around :attr:`node_idx` given an edge mask
:attr:`edge_mask`.
Args:
node_idx (int): The node id to explain.
edge_index (LongTensor): The edge indices.
edge_mask (Tensor): The edge mask.
y (Tensor, optional): The ground-truth node-prediction labels used
as node colorings. (default: :obj:`None`)
threshold (float, optional): Sets a threshold for visualizing
important edges. If set to :obj:`None`, will visualize all
edges with transparancy indicating the importance of edges.
(default: :obj:`None`)
**kwargs (optional): Additional arguments passed to
:func:`nx.draw`.
:rtype: :class:`matplotlib.axes.Axes`, :class:`networkx.DiGraph`
"""
assert edge_mask.size(0) == edge_index.size(1)
if node_idx is not None:
# Only operate on a k-hop subgraph around `node_idx`.
subset, edge_index, _, hard_edge_mask = k_hop_subgraph(
node_idx, self.__num_hops__(), edge_index, relabel_nodes=True,
num_nodes=None, flow=self.__flow__())
edge_mask = edge_mask[hard_edge_mask]
subset = subset.tolist()
if y is None:
y = torch.zeros(edge_index.max().item() + 1,
device=edge_index.device)
else:
y = y[subset].to(torch.float) / y.max().item()
y = y.tolist()
else:
subset = []
for index,mask in enumerate(edge_mask):
node_a = edge_index[0,index]
node_b = edge_index[1,index]
if node_a not in subset:
subset.append(node_a.item())
if node_b not in subset:
subset.append(node_b.item())
y = [y for i in range(len(subset))]
if threshold is not None:
edge_mask = (edge_mask >= threshold).to(torch.float)
data = Data(edge_index=edge_index, att=edge_mask, y=y,
num_nodes=len(y)).to('cpu')
G = to_networkx(data, edge_attrs=['att']) # , node_attrs=['y']
mapping = {k: i for k, i in enumerate(subset)}
G = nx.relabel_nodes(G, mapping)
kwargs['with_labels'] = kwargs.get('with_labels') or True
kwargs['font_size'] = kwargs.get('font_size') or 10
kwargs['node_size'] = kwargs.get('node_size') or 800
kwargs['cmap'] = kwargs.get('cmap') or 'cool'
pos = nx.spring_layout(G)
ax = plt.gca()
for source, target, data in G.edges(data=True):
ax.annotate(
'', xy=pos[target], xycoords='data', xytext=pos[source],
textcoords='data', arrowprops=dict(
arrowstyle="->",
alpha=max(data['att'], 0.1),
shrinkA=sqrt(kwargs['node_size']) / 2.0,
shrinkB=sqrt(kwargs['node_size']) / 2.0,
connectionstyle="arc3,rad=0.1",
))
nx.draw_networkx_nodes(G, pos, node_color=y, **kwargs)
nx.draw_networkx_labels(G, pos, **kwargs)
return ax, G
def explain_graph(self, data, **kwargs):
self.model.eval()
self.__clear_masks__()
x, edge_index, batch = data.x, data.edge_index, data.batch
num_edges = edge_index.size(1)
# Only operate on a k-hop subgraph around `node_idx`.
x, edge_index, _, hard_edge_mask, kwargs = self.__subgraph__(node_idx=None,x=x, edge_index=edge_index, **kwargs)
# Get the initial prediction.
with torch.no_grad():
log_logits = self.model(data, **kwargs)
probs_Y = torch.softmax(log_logits, 1)
pred_label = probs_Y.argmax(dim=-1)
self.__set_masks__(x, edge_index)
self.to(x.device)
if self.node:
optimizer = torch.optim.Adam([self.node_feat_mask, self.edge_mask],
lr=self.lr)
else:
optimizer = torch.optim.Adam([self.edge_mask], lr=self.lr)
epoch_losses=[]
for epoch in range(1, self.epochs + 1):
epoch_loss=0
optimizer.zero_grad()
if self.node:
h = x * self.node_feat_mask.view(1, -1).sigmoid()
log_logits = self.model(data, **kwargs)
pred = torch.softmax(log_logits, 1)
loss = self.__graph_loss__(pred, pred_label)
loss.backward()
optimizer.step()
epoch_loss += loss.detach().item()
epoch_losses.append(epoch_loss)
edge_mask = self.edge_mask.detach().sigmoid()
print(edge_mask)
self.__clear_masks__()
return edge_mask,epoch_losses
def __repr__(self):
return f'{self.__class__.__name__}()'
参考:https://towardsdatascience.com/how-can-we-explain-graph-neural-network-5031ea127004
接下来使用图分类的数据集和模型测试该类,以下是测试样例。
首先加载数据集,定义网络并完成模型训练,注意模型接收的是data,而非节点特征和边,这是为了方便图分类任务中的batch操作:
import os.path as osp
import torch
import torch.nn.functional as F
from torch.nn import Sequential, Linear, ReLU
from torch_geometric.datasets import TUDataset
from torch_geometric.data import DataLoader
from torch_geometric.nn import GINConv, global_add_pool
path = osp.join(osp.dirname(osp.abspath('')), '..', 'data', 'MUTAG')
dataset = TUDataset(path, name='MUTAG').shuffle()
test_dataset = dataset[:len(dataset) // 10]
train_dataset = dataset[len(dataset) // 10:]
test_loader = DataLoader(test_dataset, batch_size=128)
train_loader = DataLoader(train_dataset, batch_size=128)
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
num_features = dataset.num_features
dim = 32
nn1 = Sequential(Linear(num_features, dim), ReLU(), Linear(dim, dim))
self.conv1 = GINConv(nn1)
self.bn1 = torch.nn.BatchNorm1d(dim)
nn2 = Sequential(Linear(dim, dim), ReLU(), Linear(dim, dim))
self.conv2 = GINConv(nn2)
self.bn2 = torch.nn.BatchNorm1d(dim)
nn3 = Sequential(Linear(dim, dim), ReLU(), Linear(dim, dim))
self.conv3 = GINConv(nn3)
self.bn3 = torch.nn.BatchNorm1d(dim)
nn4 = Sequential(Linear(dim, dim), ReLU(), Linear(dim, dim))
self.conv4 = GINConv(nn4)
self.bn4 = torch.nn.BatchNorm1d(dim)
nn5 = Sequential(Linear(dim, dim), ReLU(), Linear(dim, dim))
self.conv5 = GINConv(nn5)
self.bn5 = torch.nn.BatchNorm1d(dim)
self.fc1 = Linear(dim, dim)
self.fc2 = Linear(dim, dataset.num_classes)
def forward(self, data):
x, edge_index, batch = data.x, data.edge_index, data.batch
x = F.relu(self.conv1(x, edge_index))
x = self.bn1(x)
x = F.relu(self.conv2(x, edge_index))
x = self.bn2(x)
x = F.relu(self.conv3(x, edge_index))
x = self.bn3(x)
x = F.relu(self.conv4(x, edge_index))
x = self.bn4(x)
x = F.relu(self.conv5(x, edge_index))
x = self.bn5(x)
x = global_add_pool(x, batch)
x = F.relu(self.fc1(x))
x = F.dropout(x, p=0.5, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=-1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)
for epoch in range(1, 101):
model.train()
if epoch == 51:
for param_group in optimizer.param_groups:
param_group['lr'] = 0.5 * param_group['lr']
loss_all = 0
for data in train_loader:
data = data.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, data.y)
loss.backward()
loss_all += loss.item() * data.num_graphs
optimizer.step()
以batch_size=1加载数据集,对其中的每个图训练GNNExplainer,学习edge_mask,得到可视化结果:
data_loader = DataLoader(train_dataset, batch_size=1)
for data in data_loader:
explainer = GNNExplainer(model, epochs=200)
data = data.to(device)
edge_mask,_ = explainer.explain_graph(data)
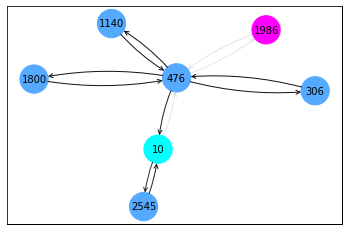
ax, G = explainer.visualize_subgraph(None, data.edge_index, edge_mask, y=data.y)
plt.show()
break