Contents
How Powerful are Graph Neural Networks?

预备知识
GNN
注:下表中GCN一行的公式包含了AGGREGATE和COMBINE两步。
| AGGREGATE | COMBINE | |
|---|---|---|
| GraphSAGE | \(a_v^{(k)}=MAX(\{ReLU(W\cdot{h_v^{(k-1)}),\forall{u\in}N(v)\}})\) | \(W\cdot{[h_v^{(k-1)},a_v^{(k)}]}\) |
| GCN(2017第四代) | \(h_v^{(k)}=ReLU(W\cdot{MEAN\{h_v^{(k-1)},\forall{u\in}N(v)\bigcup{\{v\}}\}})\) |
GCN的公式为什么可以理解为求平均?
\[H^{l+1}=\sigma(\widetilde{D}^{-\frac{1}{2}}\widetilde{A}\widetilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)})\\ =\sigma(\hat{A}H^{(l)}W^{(l)})\]参考资料:1. GraphSAGE:我寻思GCN也没我牛逼,2. 一文读懂图卷积GCN
-
\(\hat{A}\): 邻接矩阵A的归一化

-
\(\hat{A}\cdot{H}\)的含义:
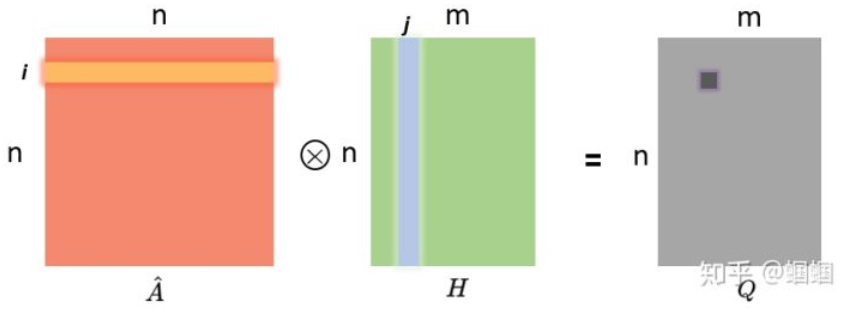
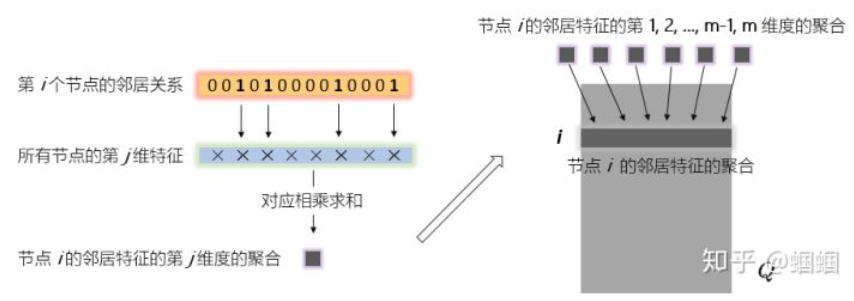
GCN聚合的理解